Die Komplexitätsklassen P und NP sind jeweils eine Menge aus Problemen. In der Klasse P befinden sich die Probleme, die in polynomieller Zeit lösbar sind, es sind Sozusagen „leichte“ Probleme. Das heißt für diese Art von Problemen existiert ein Algorithmus, der in polynomieller Zeit (also in naher Zukunft) eine Lösung findet.
In der Klasse NP befinden sich die Probleme, bei denen in polynomieller Zeit geprüft werden kann, ob es eine Lösung gibt oder nicht. Man nennt sie auch nichtdeterministische polynomielle Probleme. Das heißt, in dieser Klasse befinden sich alle Probleme, über die man eine Aussagen treffen kann, ob es eine Lösung für dieses Problem gibt oder nicht. Jedoch ist es (noch) nicht möglich, diese Probleme zu lösen.
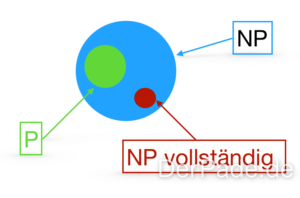
Jedes Problem in P befindet sich übrigens auch automatisch in der Klasse NP. Zusätzlich existieren in NP Probleme, über die man nicht einmal aussagen kann, dass es eine Lösung gibt, das heißt für solche Probleme existiert auch kein Algorithmus zur Berechnung der Lösung. Diese Art von Problemen befinden sich in NP-vollständig.
Die Klasse NP-vollständig enthält besonders knifflige Probleme, bei denen es bisher keine effiziente Lösung gibt. Wenn für ein Problem in dieser Klasse eine effiziente Lösung gefunden wird, gilt sie automatisch auch für alle anderen Probleme in NP und P.
Um die Unterschiede zu verdeutlichen: In P sind die Probleme effizient lösbar, in NP können Lösungen effizient überprüft werden, aber ihre Berechnung ist schwieriger. NP-vollständige Probleme stellen eine Herausforderung dar, da sie in keiner bekannten polynomiellen Zeit lösbar sind und dennoch zu NP gehören.
Die bildliche Darstellung zeigt die Hierarchie dieser Komplexitätsklassen und ihre Verbindung. Das Verständnis dieser Konzepte ist entscheidend für die Algorithmusanalyse und das Einschätzen der Effizienz von Lösungsansätzen in der Informatik.
Jetzt bist du bereit, tiefer in die Welt der algorithmischen Komplexität einzutauchen. Verfolge aktuelle Entwicklungen und bleibe neugierig, denn die Informatik hält stets neue Herausforderungen und Lösungen bereit.
Weitere Beiträge aus dieser Serie
- Binäre Suchbäume in der Informatik einfach erklärt
- Durchsuchen von Array-Listen - Lineare und Binäre Suche
- Sequentielle Datentypen
- Algorithmische Techniken - Brute Force, Greedy, Teile und Herrsche, Dynamische Programmierung und Backtracking
- Lazy Evaluation und Streams
- Die Liste als abstrakter Datentyp
- Korrektheitsbeweise von Klassen und Schleifen
- Der Graph als abstrakter Datentyp