Der Graph als abstrakter Datentyp

In diesem Beitrag werden wir uns mit Graphen als abstrakte Datentypen beschäftigen. Ein Graph besteht aus einer Menge von Knoten und Kanten. Ein Knoten speichert die eigentlichen Daten und wird auch „Ecke” oder „Vertex” genannt. Eine Kante verbindet Knoten mit einander und wird auch „Edge” genannt.

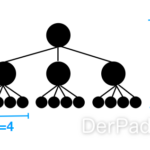
Ein einfacher Graph könnte beispielsweise folgendermaßen definiert sein. Dieser Graph ist zusammenhängend, ungerichtet und besitzt demnach auch keine Zyklen.

Der Graph als abstrakter Datentyp Einfacher Graph

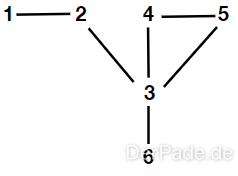Knoten: 1, 2,3, 4, 5,6

Kanten:

Verketteter Graph

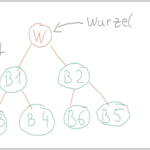
Die Implementierung eines Verketteten Graphen gleicht der einer Implementierung für einen verketteten Baum. Es existiert – anders als bei einer Baumstruktur – kein definierter Startknoten. Außerdem gibt es keine Beschränkung in der Anzahl von Elternknoten. Dabei entsteht ein Sogenannter gerichteter Graph. Dies wurde in der Abbildung durch grüne Pfeile ersichtlich gemacht.

Ein einfacher verketteter gerichteter Graph.

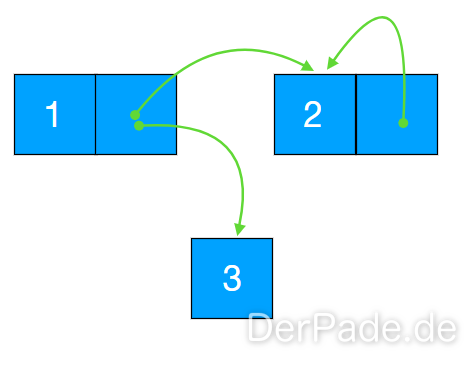
Der Unterschied zwischen einem gerichteten und ungerichteten Graphen liegt in seiner Kantendefinition. Bei einem gerichteten haben diese eine Richtungsangabe. Die Kanten (1, 2) und (2, 1) sind daher unterschiedliche Kanten, da sie jeweils in eine andere Richtung zeigen. Anders sieht dies bei einem ungerichteten Graphen aus, denn durch die fehlende Richtungsangabe sind die Kanten (1,2) und (2,1) gleich und es gilt:

∀ a,b ∈ V:(a,b) ∈ E →(b,a) ∈ E

Zyklen

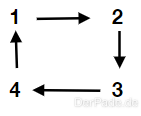
Zyklen beschreiben einen Pfad von einem Knoten zu sich selbst. In einem ungerichteten Graph darf jede Kante deshalb nur in eine Richtung auf diesem Pfad auftauchen.

Einen Graph, der keine Zyklen enthält, nennt man azyklischer Graph.

Einen Graph ist zusammenhängend, wenn zwischen jedem Paar von Knoten mindestens eine Kante existiert. Zusätzlich unterscheidet man bei einem gerichteten Graphen zwischen schwach und stark Zusammenhängend, je nach dem, ob eine Kante in beide Richtungen existiert oder nur in eine Richtung.

Ein Beispiel für einen nicht zusammenhängenden Graphen, welcher in Zusammenhangs-Komponenten zerfällt.

Merke: Bei einer Tiefen- oder Breitensuche eines zyklischen Graphen entsteht eine Endlosschleife, die man nur durch dynamisches Programmieren umgehen kann. Dabei merkt man sich die bereits besuchten Knoten und überspringt diese gegebenenfalls.