Baum Datenstruktur
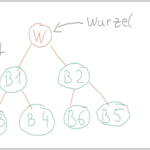
In diesem Beitrag wird die Baum Datenstruktur als abstrakter Datentyp betrachtet. Ein Baum enthält üblicherweise drei Arten von Knoten:
- Wurzelknoten: Ist der Ursprung und besitzt keine Elternknoten, dafür aber beliebig viele Kindknoten.
- Innerer Knoten: Befinden sich im Inneren eines Baums und hab einen Eltern Knoten und mindestens einen Kindknoten.
- Äußere Knoten: nennt man auch Blattknoten. Sie haben keine weiteren Kindknoten mehr.
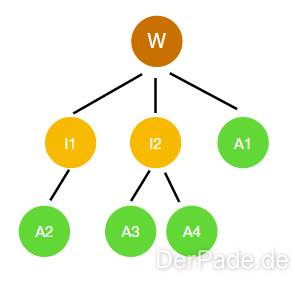
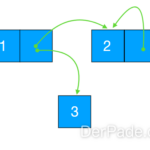
Verketteter Baum
Ein verketteter Baum ist vergleichbar mit einer verketteten Liste. Unsere Knoten sind Objekte, die ihre Kindknoten als Referenz speichern. Eine sehr wichtige Bedingung ist, dass keine Referenz auf den Wurzelknoten zurück führen darf, da so ein Kreis entsteht und ein Kreis ist laut Definition kein Baum. Außerdem muss zu jedem anderen Knoten genau eine Referenz führen, das heißt, der Baum muss zusammenhängend sein. Ein abgefallenes Blatt zählt demnach nicht mehr zum Baum.
Tiefensuche
Die Tiefensuche wird genutzt, um eine Baumstruktur zu durchsuchen. Begonnen wird dabei bei der Wurzel, falls die Wurzel das gesuchte Element ist, ist die Suche beendet. Andernfalls wird das erste Kind vollständig durchsucht, danach das Zweite usw. Wenn keins der Kindknoten den Wert enthält, kann das gesuchte Element bzw. der gesuchte Wert nicht gefunden werden.
Effizienzklasse: O(n)
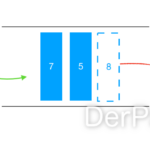
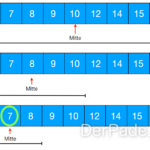
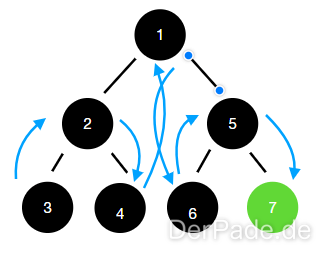
Beispiel: Wir suchen die „7″ in unserem Baum.
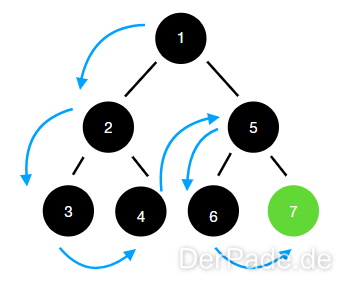
Der hier abgebildete Baum in Verbindung mit der pre-order Tiefensuche stellt den “worst-case” dar, weil der gesuchte Wert erst beim letzten Knoten gefunden wird.
Bei der post-order Traversierung werden die Kindknoten vor den Eltern Knoten durchsucht.
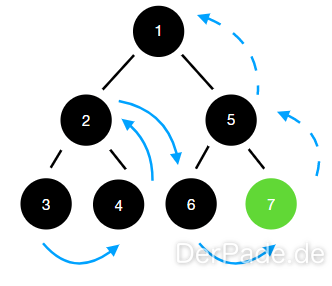
Bei der in-order Traversierung werden die Elternknoten zwischen den Kindknoten durchsucht. Diese Methode wird hauptsächlich bei Binärbäumen genutzt.
Breitensuche
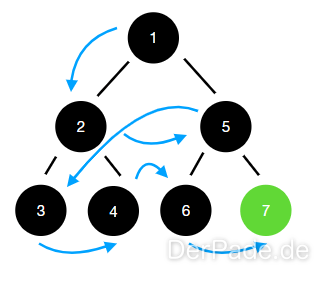
Das Gegenstück zur Tiefersuche ist die Breitensuche. Dieses Suchverfahren durchsucht die Baumstruktur Ebene für Ebene.
Breiten- und Tiefensuche im Vergleich
Beide Suchverfahren sind Spezialfälle der linearen Suche. Der Unterschied liegt in der Aufzählung der Elemente, wodurch unterschiedlich viel Speicherplatz verbraucht wird.
- Speicher Verbrauch von dfs (Tiefensuche): O(n)
- Speicher Verbrauch bfs (Breitensuche): O(n)
Der Speicherverbrauch beider Methoden sieht gleich aus, gilt aber für unterschiedliche “worst cases”.
Vollständige Bäume
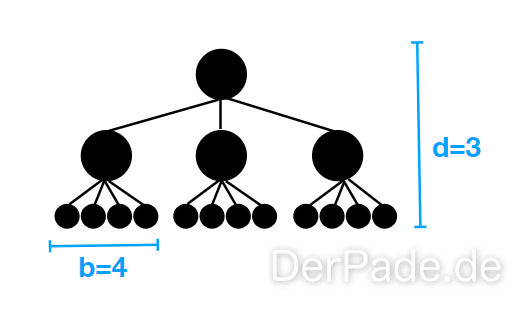
Um eine bessere Aussage über die “use-cases” (Anwendungsfälle) der beiden Suchverfahren zu treffen, betrachten wir den vollständigen Baum. Ein Baum ist vollständig wenn folgende Kriterien erfüllt sind:
- Jeder Knoten bis zur Tiefe d- 1 hat genau b Kinder.
- Jeder Knoten der Tiefe d ist ein Blatt Knoten.
Bei einem vollständigen Baum schneidet die Tiefensuche deutlich besser ab, denn die maximale Tiefe d bestimmt hier den Speicher Verbrauch: O(d) statt O(b^d)
Iterative Suche
Die iterative Suche ist quasi eine Tiefensuche mit der Ausnahme, dass die Tiefe beschränkt wird.
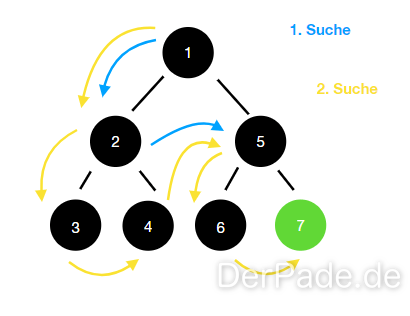
Laufzeit: 0 (n) Speicher: 0 (d)
Die Laufzeit ist um einen Konstanten Faktor c <5 Schlechter als ber dfs oder bfs. Der Speicherverbrauch ist mit 0 (d) aber nicht besser. wo liegt nun der Vorteil der iterativen Suche?
Die Antwort ist iteratives Feedback, welche genutzt werden kann, um dem Benutzer beispielsweise Rückmeldung zu geben oder beim nächten iterativen Schritt den besten Pfad zu wählen.
Weitere Beiträge aus dieser Serie
- Binäre Suchbäume in der Informatik einfach erklärt
- Durchsuchen von Array-Listen - Lineare und Binäre Suche
- Sequentielle Datentypen
- Algorithmische Techniken - Brute Force, Greedy, Teile und Herrsche, Dynamische Programmierung und Backtracking
- Lazy Evaluation und Streams
- Die Liste als abstrakter Datentyp
- Korrektheitsbeweise von Klassen und Schleifen
- Der Graph als abstrakter Datentyp