In diesem Beitrag beschäftigen wir uns mit den gängigen algorithmischen Techniken wie Brute Force, Gier, Teile und Herrsche und der dynamischen Programmierung.
Brute Force
Bei dieser Technik wird völlig willkürlich versucht eine Lösung für ein bestehendes Problem zu finden. Der Algorithmus endet erst, wenn die Menge der möglichen Lösungen für das Problem erschöpft ist (keine Lösung gefunden), oder die Lösung für das gegebene Problem gefunden wurde. Ein gutes Beispiel ist hier das Raten von Passwörtern. Dabei wird eine Liste von Permutationen aus validen Zeichen erstellt und abgefragt.
Vorteile:
- Der Algorithmus ist sehr robust.
- Einfach zu implementieren
- Findet irgendwann garantiert die Lösung (falls die Lösung sich in der Menge der möglichen Lösungen befindet)
Nachteile:
- Bei großen Eingabemengen sehr langsam.
- Eigentlich ein „dummer” Algorithmus.
Brute Force ist quasi eine Schleife, die über alle möglichen Lösungen läuft, weshalb die Laufzeit in der Effizienzklasse von O(n) liegt.
Greedy
Greedy agiert durch eine Heuristik ein wenig intelligenter als Brute Force. Der Algorithmus startet an einer zufälligen Stelle und geht immer in die Richtung, welche den kürzesten Weg zu Ziel beinhaltet. Der Algorithmus endet, wenn alle nächstmöglichen Lösungen ihn weiter wegbringen vom Ziel.
Vorteile:
- Ist schnell, wenn Heuristik schnell zu prüfen ist.
- Kann auch bei großen Eingabemengen schnell sein.
Nachteile:
- Nur möglich, wenn man eine Heuristik implementieren kann.
- Kann unter Umständen zwar eine Lösung finden, aber wenn mehrere Lösungen existieren, kann es vorkommen, dass nicht die optimalste Lösung gefunden wurde, denn der Algorithmus endet, sobald irgendeine Lösung gefunden wurde.
Teile und Herrsche
Dieser Algorithmus teilt das Probleme in “n”-Teile auf und zwar so lange, bis die Lösung für das Teilproblem trivial ist. Danach werden alle „n”-Teillösungen wieder kombiniert, bis das ursprüngliche Problem mit der Gesamtlösung gelöst ist. Die Voraussetzung für diesen Algorithmus ist, dass das gegebene Problem sich aufteilen lässt.
Effizienz klasse:
- Aufteilen: O(log n)
- Zusammenführen: O(n)
- Gesamt: O(n * log n)
Ein typisches Beispiel für diesen Algorithmus ist die Generierung eines Labyrinths.
Dynamische Programmierung
Bei der dynamischen Programmierung macht man sich die Vorteile eines „Caches” zu nutzen, indem man Teilergebnisse zwischenspeichert und sie nicht erneut berechnen muss. Beispielsweise kann mit so einem Cache eine effizientere Variante realisiert werden, um die Fibonacci-Folge zu berechnen.
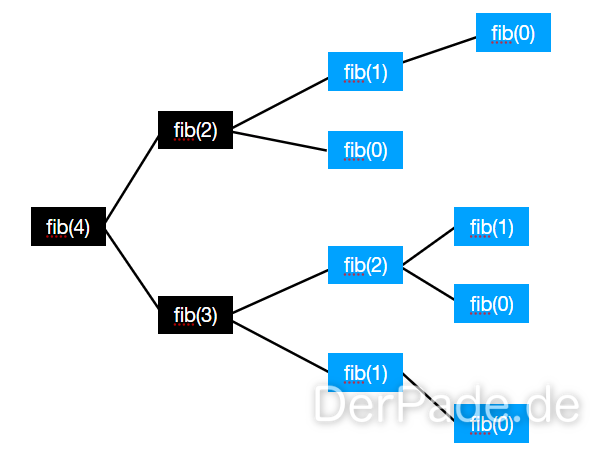Eine stupide Implementierung der Fibonacci-Folge würde auch die Berechnung für die blauen Knoten durchführen. Bei der dynamischen Programmierung schauen wir vor der Berechnung nach, ob das Teilergebnis bereits im Cache liegt.
Effizienzklasse:
- Ohne Cache: O(2n)
- Mit Cache: O(n)
Backtracking
Backtracking ist eine sinnvolle Methode zum Finden einer Lösung, wenn ungültige Lösung schnell identifiziert werden können. Bei dieser Methode geht man wie folgt vor:
- Finde die erste Möglichkeit für den ersten Lösungsschritt.
- Wähle die erste Möglichkeit für den zweiten Lösungsschritt.
- Sobald sich erkennen lässt, dass der Teillösungsweg ungültig ist oder wird, muss ein Schritt zurück gegangen werden (“trackback”).
Mit diesem Prinzip kann man definitiv eine Aussage darüber treffen, ob eine Lösung existiert oder nicht. Backtracking arbeitet nach dem Prinzip der Tiefensuche.
Weitere Beiträge aus dieser Serie
- Binäre Suchbäume in der Informatik einfach erklärt
- Durchsuchen von Array-Listen - Lineare und Binäre Suche
- Sequentielle Datentypen
- Algorithmische Techniken - Brute Force, Greedy, Teile und Herrsche, Dynamische Programmierung und Backtracking
- Lazy Evaluation und Streams
- Die Liste als abstrakter Datentyp
- Korrektheitsbeweise von Klassen und Schleifen
- Der Graph als abstrakter Datentyp
